Let's illustrate edges of the self-attention graph $G$ with adjacency matrix ${\bf A}$:

A representation $\Gamma \in \mathbb{R}^{n \times d}$, $d > 0$, of a sequence $x_1,\ldots,x_n$ is permutation equivariant if $$ \Gamma(x_1,\ldots,x_n)_{i,\cdot} = \Gamma(x_{\pi_1},\ldots,x_{\pi_n})_{\pi^{-1}_i,\cdot}, \quad \forall \pi \in \Pi_n, i = 1,\ldots,n, $$ where $\Pi_n$ is the set of all permutations of the sequence $(1,\ldots,n)$ and $\pi^{-1}$ its inverse.
Now consider creating a new sequence $x'_1,\ldots,x'_n$ by adding a positional feature $$x'_i = (x_i,i).$$
Now, a permutation-equivariant representation $$\Gamma'(x'_1,\ldots,x'_n)_{i,\cdot} = \Gamma'(x'_{\pi_1},\ldots,x'_{\pi_n})_{\pi^{-1}_i,\cdot}, \quad \forall \pi \in \Pi_n, i =1,\ldots,n$$ is a set representation on $x'_1,\ldots,x'_n$.
However, note that $\Gamma'$ may be a sequence representation of $x_1,\ldots,x_n$, if $$\exists \pi \in \Pi_n, \: \text{ s.t. } \Gamma'((x_1,1),\ldots,(x_n,n))_{i,\cdot} \neq \Gamma'((x_{\pi_1},1),\ldots,(x_{\pi_n},n))_{\pi^{-1}_i,\cdot},\quad i=1,\ldots,n.$$
Consider the adding positional indices to the original set (bag) of words:
Clearly, we could learn a set representation that would represent the original data as a sequence
PS: Note that $\Gamma'$ is permutation-equivariant if it sorts the elements of the set based on their positions (2nd dimension), and then learn a sequence representation.
Interestingly, it is $\Gamma'$ who should decide if it wants to be a set or sequence representation:
Consider the following self-attention graph $G = (V,E,X')$, with
Consider the sentence
We are going to add $\text{pos}(i)$ as a positional encoding feature of the $i$-th word in the sequence.
The feature set of the vertices of our self-attention graph is $$X'=\{(x_\text{avocado}, pos(4)), (x_\text{like}, pos(3)), (x_\text{thank}, pos(5)), (x_\text{I},pos(1)), (x_\text{don't},pos(2))\}$$
Let's illustrate edges of the self-attention graph $G$ with adjacency matrix ${\bf A}$:

Note that the edges of $G$ are a function of the input sequence $x'_1,\ldots,x'_n$.
Proposition: If $\Gamma_G({\bf A}_{1,1}, {\bf A}_{1,2},\ldots,{\bf A}_{n,n},x'_1,\ldots,x'_n)$ is a graph representation of $G$.
Proof: If $\Gamma_G({\bf A}_{1,1}, {\bf A}_{1,2},\ldots,{\bf A}_{n,n},x'_1,\dots,x'_n)$ is a graph representation it must be equivariant to joint permutations: $$\Gamma_G({\bf A}_{1,1}, {\bf A}_{1,2},\ldots,{\bf A}_{n,n},x'_1,\ldots,x'_n)_{i,\cdot} = \Gamma_G({\bf A}_{\pi_1,\pi_1}, {\bf A}_{\pi_1,\pi_2},\ldots,{\bf A}_{\pi_n,\pi_n},x'_{\pi_1},\ldots,x'_{\pi_n})_{\pi^{-1}_i,\cdot}, \: \forall \pi \in \Pi_n.$$ Since ${\bf A}_{\pi_i,\pi_j} = \alpha(x'_{\pi_i},x'_{\pi_j}; \cdot)$, the representation $\Gamma_G$ only depends on $x'_1,\ldots,x'_n$ and is, by its definition, invariant to a shuffling of the input sequence $x'_{\pi'_1},\ldots,x'_{\pi'_n}$, $\forall \pi' \in \Pi_n$.
The transformer architecture was first introduced by (Vaswani et al., 2017)
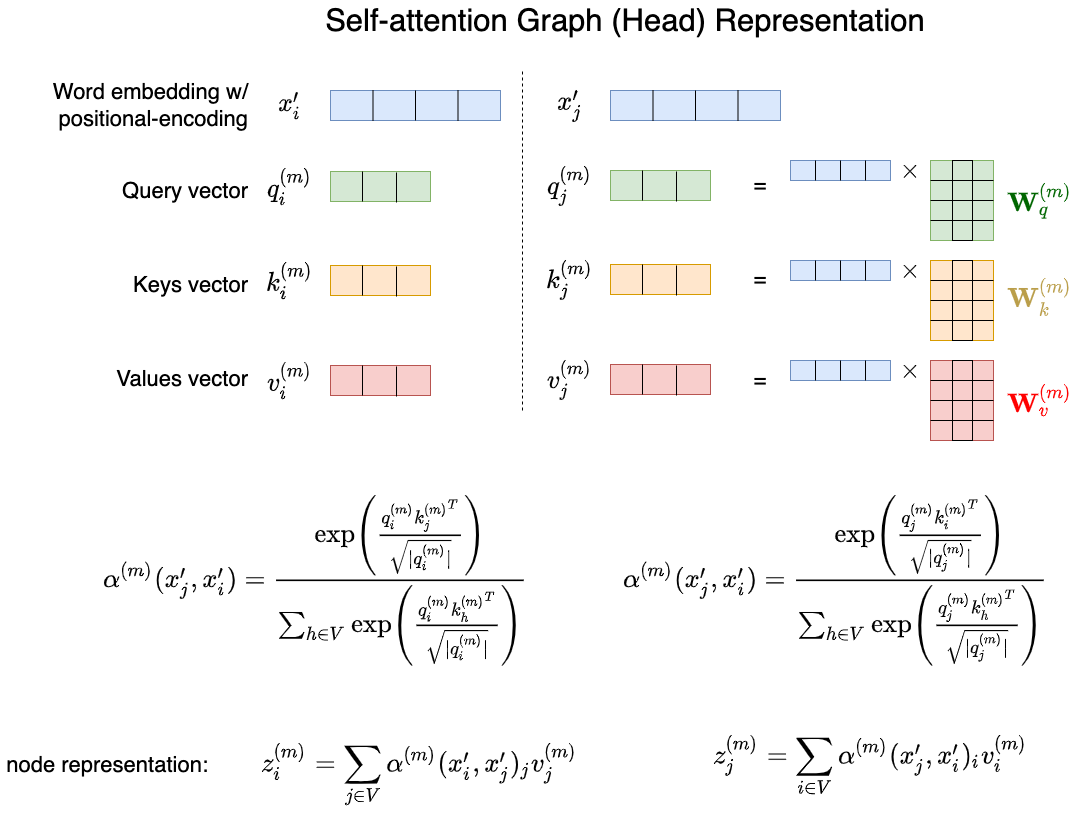
The key idea behind the Transformer model is self-attention with positional encoding:
The $m$-th self-attention is a function $\alpha^{(m)}(\cdot,\cdot;\cdot) \in (0,1)$.
A Transformer creates multiple self-attention graphs $G_1,\ldots,G_M$. Each graph is called a head.
The transformer model handles variable-sized inputs through these graphs $G_1,\ldots,G_M$.
The following illustrates the operations:

In our CNN class, we have seen that max-pooling can create a permutation invariant layer.
That is, given a sequence (input vector) $$ {\bf x} = (x_1,\ldots,x_n) $$ and a permutation $\pi$ over the integers $\{1, 2,\ldots,n\}$ such that $\pi \circ {\bf x} = (x_{\pi_1},\ldots,x_{\pi_n})$ is the correspondingly permuted version of ${\bf x}$, the max-pooling function over ${\bf x}$ has the property that $$ \Gamma_\text{max-pooling}({\bf x}) = \Gamma_\text{max-pooling}(\pi\circ{\bf x}), \quad \forall \pi \in \mathbb{S}_n, $$ where $\mathbb{S}_n$ is the symmetric group of order $n$ (which defines a set of all permutations over the integers $\{1, 2,\ldots,n\}$).
Note that max-pooling is also the same basic operation for any value of $n > 0$ (i.e., it operates over any-size inputs).
In this lecture we will see that max pooling is one of the simplest examples of a class of neural networks that can ensure permutation invariances.
However, max-pooling (min-pooling) is a heuristic that is not learnable.
Q: What other heuristics are permutation-invariant and can operate on any-size inputs?
Task:
Consider a set of random variables over a countable space $\Omega$: $$ \{X_{j}\}_{j=1}^n,\qquad X_j \in \Omega $$
Joint probability distributions are only defined over ordered sequences (vectors). That is, the joint probability $P$ is defined as $$ P: \Omega^n \to [0,1] $$
Q: How should we define their joint probability distribution as a set?
Definition: The probability distribution $P$ must be such that $$ P(X_1,\ldots,X_n) = P(X_{\pi_1},\ldots,X_{\pi_n}), $$ for any permutation $\pi$ of $\{1,\ldots,n\}$.
The property of a probability distribution $P$ to be invariant under permutations is also known as exchangeability, since exchanging the random variables $X_{\pi_1},\ldots,X_{\pi_n}$ does not change their joint probability distribution.
The noise transfer theorem (noise outsourcing) allows us to decompose $P(X_1,\ldots,X_n)$ as a
A set representation $\Gamma(x_1,\ldots,x_n)$, which has the property that $\forall \pi \in \mathbb{S}_n$, $$\Gamma(x_1,\ldots,x_n) = \Gamma(x_{\pi_1},\ldots,x_{\pi_n})$$
And a deterministic function $\alpha:\Omega^n \to [0,1]$
Assume we have an infinite sequence of exchangeable variables. Then:
De Finetti's theorem: The probability distribution of any infinite sequence of $\{0, 1\}$-valued exchangeable random variables can be described as a mixture of conditionally independent distributions: $$ P(X_1,X_2,\ldots) = \int_\theta \prod_{i=1}^\infty P(X_i| \theta) d\!P(\theta). $$
This is the inspiration for a lot of Bayesian models: e.g., Latent Dirichlet Allocation.
Infinite exchangeability in noise transfer representation: $$ P(X_1,X_2,\ldots) = \int_\theta \prod_{i=1}^\infty \rho \left(\Gamma_\theta(X_i)\right) d\!P(\theta). $$
Note that this is just applying a representation over all set elements.
Consider the following set distribution:
Q: Assume $n$ is very large but finite. Can we arbitrarily approximate (or describe) $$P(X_1,\ldots,X_n)$$ using De Finetti's conditional independent mixture model? I.e., $$ P(X_1,\ldots,X_n) \approx \int_\theta \prod_{i=1}^n P(X_i| \theta) d\!P(\theta). $$
A: No, since no matter how large $n$ is, $P(X_2 = \text{tuna}|X_1=\text{tuna}) = 0$ but $P(X_2 = \text{tuna})>0$, and these two conditions cannot be represented by a mixture of conditionally independent distributions.
A good read on the topic is Diaconis, Finite forms of de Finetti’s theorem on exchangeability, Synthese 1977
Consider the following scenario:
The pair $X_1, X_2$ is exchangeable.
Q: Can we arbitrarily approximate (or describe) $$P(X_1, X_2)$$ using De Finetti's conditional independent mixture model? I.e., $$ P(X_1 = e_1, X_2 = e_2) \approx \int_\theta \prod_{i=1}^n P(X_i = e_i| \theta) d\!P(\theta), $$ for each sequence of zeros and ones $\{e_i\}_{i=1}^2$?
A: No, if there exists $P(\theta)$ such that $$ 0 = P(X_1 = 1, X_2 = 1) = \int_\theta P(X_1 = 1| \theta) P(X_2 = 1| \theta) d\!P(\theta), $$ then necessarily $P(\theta)$ puts mass 1 at the point when $P(X_1 = 1| \theta) = P(X_2 = 1| \theta) = 0$, which is also the point when $P(X_1 = 0| \theta) = P(X_2 = 0| \theta) = 1$, so we cannot have $$ 0 = P(X_1 = 0, X_2 = 0) = \int_\theta P(X_1 = 0| \theta) P(X_2 = 0| \theta) d\!P(\theta). $$
Since we have reached a contradiction we cannot use De Finetti's conditional independent mixture model.
Finite exchangeability requires a more complex representation: $$ P(X_1,\ldots, X_n) = \rho\left(\Gamma(X_1,\ldots,X_n)\right) $$ such that $\forall \pi \in \mathbb{S}_n$, $$\Gamma(x_1,\ldots,x_n) = \Gamma(x_{\pi_1},\ldots,x_{\pi_n})$$
Q: Can we learn a representation $\Gamma(X_1,\ldots,X_n)$ using a MLP?
A: Yes, MLPs are universal approximators. However, with finite data, the learned MLP will probably be permutation sensitive.
Q: How can we enforce permutation-invariant representations for sets of arbitrary sizes?
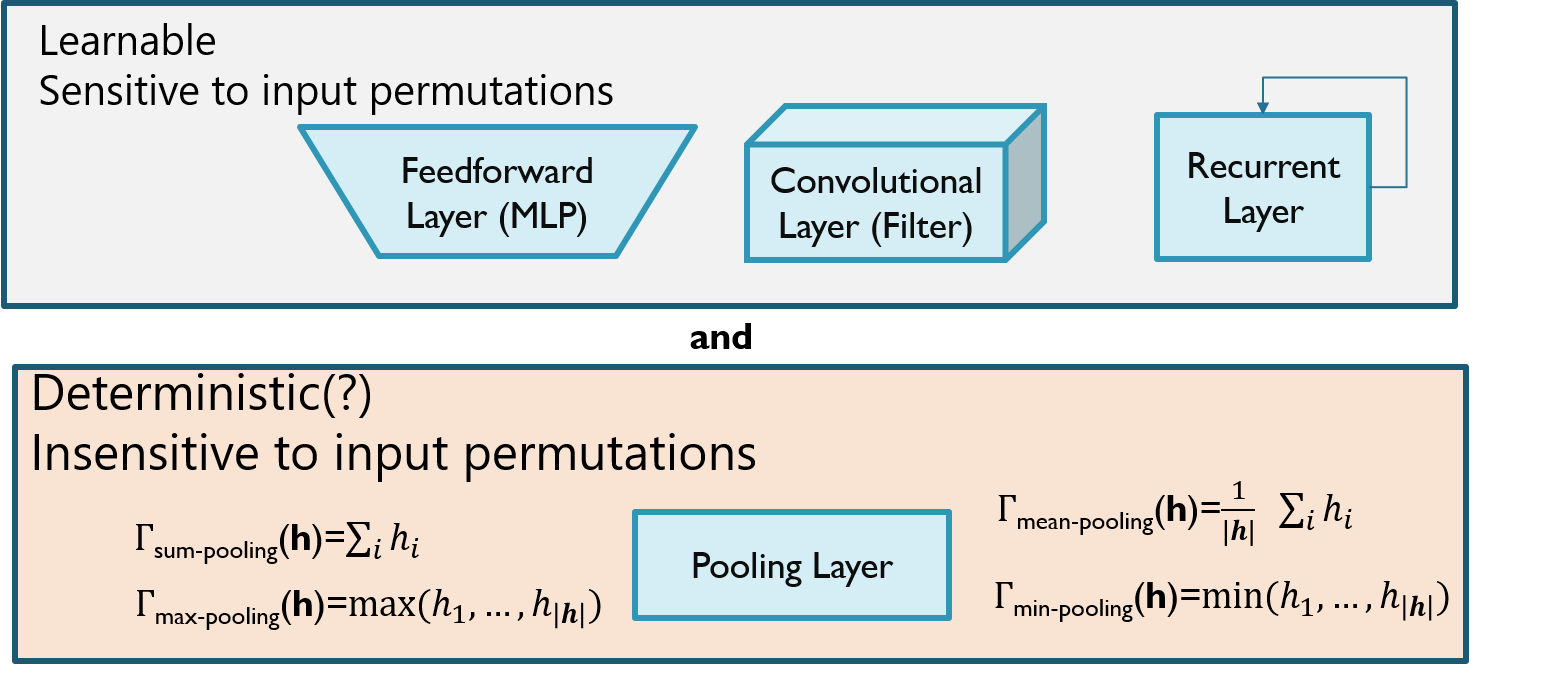
We would like to learn these pooling operations, rather than relying on heuristics.
Murphy et al., 2019 defines the permutation-invariant representation as: $$ \tag{1} \label{eq:dbarf} \Gamma({\bf x}; \boldsymbol{\theta}^{(f)}) = \frac{1}{n!} \sum_{\pi \in \mathbb{S}_n} \vec{f}(\pi \circ {\bf x} ; \boldsymbol{\theta}^{(f)}), $$ where $\vec{f}$ is any permutation-sensitive function (MLP, CNN, RNN...). We will call this representation Janossy pooling.
All existing approaches to learnable permutation representations are special cases of Equation (1).
Exercise:
Learning the representation:
There are three main approaches to make Equation (3) computationally tractable.
A good canonical order must be correlated with the task.
Q: Give an example where a canonical order will fail
A: Consider a two-dimensional random variable input $X_i = (A_i,B_i)$. Assume we decide to sort by $A_i$ but the target label depends only on $B_i$, where $A_i$ is independent of $B_i$.
Theorem 2.1 (Murphy et al., 2019): For any $k\in\mathbb{Z}^+$, define $\mathcal{F}_{k}$ as the set of all permutation invariant functions that can be represented by Equation (3) with $k$-ary dependencies.
DeepSets: $k=1$ (Unary) dependencies are what we have earlier described as mean-pooling $$\Gamma_\text{mean-pooling}({\bf x}; \boldsymbol{\theta}) = \frac{1}{n} \sum_{j=1}^n \vec{f}(x_j; \boldsymbol{\theta})$$ which is used by existing Graph Neural Network (GNN) models, as we will se in our next class.
DeepSets (Zaheer et al., 2017) proves that models using $k=1$-ary representation can learn arbitrary dependencies in the input data as long as its output is coupled with an universal approximator non-linearity. Corollary 2.1 of Murphy et al., 2019 shows that this non-linearity is in charge of undoing the sum of $k=1$ to model higher-order $k$-ary dependencies, $k > 1$. In practice, neural networks not always can recover $k$-ary dependencies from unary Janossy pooling.
Set Transformer: $k=2$ (Pairwise) dependencies can be learned with the Transformer archtecture (Lee et al., 2019) (which we will cover later in the tutorial)
Set Twister: Set Twister is an alternative $k=2$ (pairwise) approach to the transformer that is computationally cheaper but with empirical similar performance (Zhou et al., 2021)
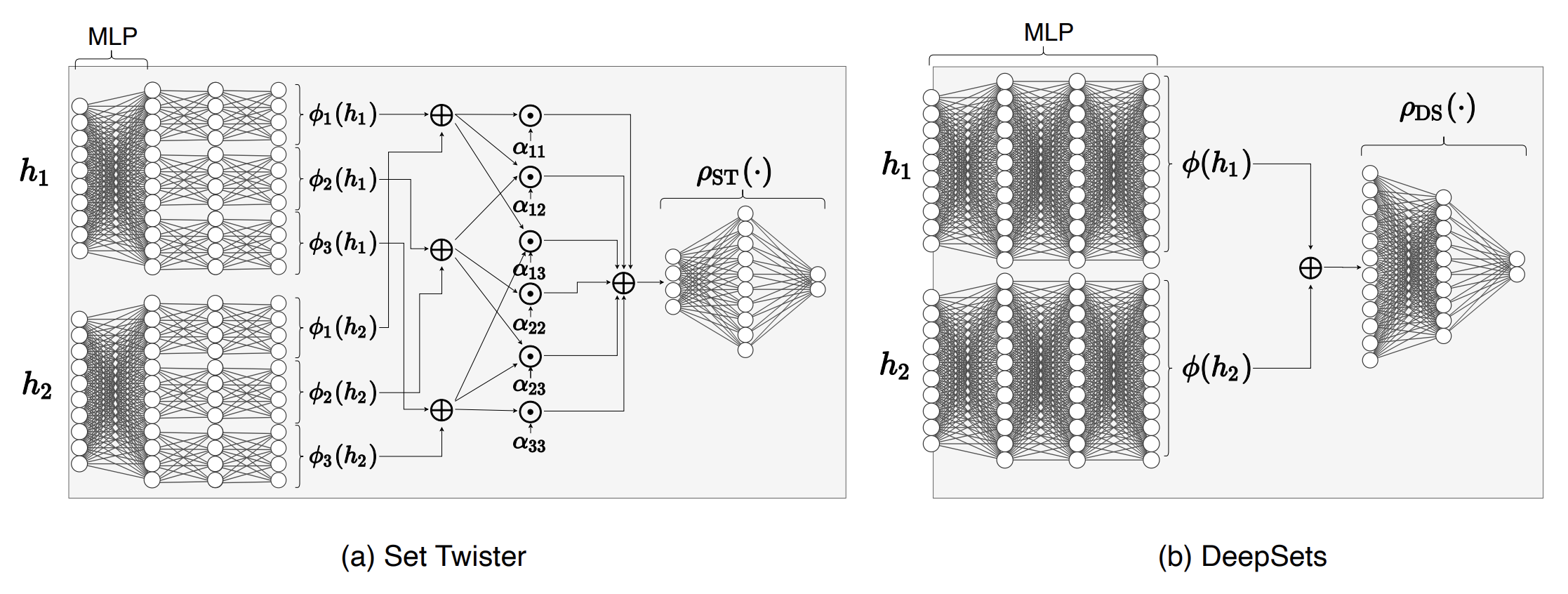
The only known tractable learnable permutation-invariant representation that makes no assumptions about the inputs is approximation using stochastic optimization.
Remember our loss function: $$L(\mathcal{D};\boldsymbol{\theta}^{(\rho)},\boldsymbol{\theta}^{(f)}) = \frac{1}{N}\sum_{i=1}^N \! L\left({\bf y}_i , \alpha\Big( \Gamma({\bf x}^{(i)};\boldsymbol{\theta}^{(f)}) ; \boldsymbol{\theta}^{(\rho)} \Big) \right),\label{eq:Loss2} \tag{5}$$ where $$\Gamma({\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}) = \frac{1}{n^{(i)}!} \sum_{\pi \in \mathbb{S}_{|{\bf x}^{(i)}|}} \!\!f(n^{(i)}, \pi \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}).\tag{6} \label{eq:janLoss2} $$
Computing the gradient of Equation $(\ref{eq:janLoss2})$ is intractable for large inputs ${\bf x}^{(i)}$, as the backpropagation computation graph branches out for every permutation in the sum. To address this computational challenge, we will use stochastic optimization.
Before we go into the details of permutation sampling, we need two results:
Note 1:. If $\textrm{X}$ is a random variable with non-zero variance, and $\alpha(\cdot)$ is a non-linear function, then it is possible that $E[\alpha(\textrm{X})] \neq \alpha(E[\textrm{X}])$.
Note 2: (Jensen's inequality) If $\textrm{X}$ is a random variable and $\alpha(\cdot)$ is a convex function, then $E[\alpha(\textrm{X})] \geq \alpha(E[\textrm{X}])$. Thus, minimizing $E[\alpha(\textrm{X})]$ is a surrogate to minimizing $\alpha(E[\textrm{X}])$.
Recall that we were interested in: $$\tag{7} \label{eq:janLoss3} \Gamma({\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}) = \frac{1}{n^{(i)}!} \sum_{\pi \in \mathbb{S}_{|{\bf x}^{(i)}|}} \!\!\vec{f}(n^{(i)}, \pi \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}).$$
Permutation sampling. Consider replacing the sum with the estimate $$\tag{8} \label{eq:JanStochOpt} \hat{\Gamma}({\bf x} ; \boldsymbol{\theta}^{(f)} ) = \vec{f}(n_{\textrm{s}}, \textrm{s}\circ{\bf x}; \boldsymbol{\theta}^{(f)}),$$ where $\textrm{s}$ is a random permutation sampled uniformly, $\textrm{s} \sim \text{Unif}(\mathbb{S}_{n})$ and $n_{\textrm{s}}$ is the length of the sequence ${\bf x}_{\textrm{s}}$.
The estimator in Equation $(8)$ is unbiased: $E_\textrm{s}[\hat{\Gamma}({\bf x} ; \boldsymbol{\theta}^{(f)} )] = \Gamma({\bf x} ; \boldsymbol{\theta}^{(f)} ).$ Note however that when $\Gamma$ is chained with another nonlinear function $\alpha$ and/or nonlinear loss $L$, the composition is no longer unbiased: $$E_\textrm{s}[L({\bf y},\alpha(\vec{f}(n_\textrm{s}, \textrm{s}\circ {\bf x}; \boldsymbol{\theta}^{(f)});\boldsymbol{\theta}^{(\alpha)}))] \neq L({\bf y},\alpha(E_\textrm{s}[\vec{f}(n_\textrm{s}, \textrm{s}\circ {\bf x}; \boldsymbol{\theta}^{(f)})];\boldsymbol{\theta}^{(\alpha)})) .$$
Definition 2.3 $\pi$-SGD (Murphy et al., 2019):
Let $\mathcal{B} =\{({\bf x}^{(1)},{\bf y}_{1}),\ldots,({\bf x}^{(B)},{\bf y}_{B})\}$ be a mini-batch sampled uniformly i.i.d. from the training data $\mathcal{D}$.
At step $t$, consider the stochastic gradient descent update
$$\label{eq:piSGD} \boldsymbol{\theta}_t = \boldsymbol{\theta}_{t-1} - \eta_t \textrm{Z}_t,$$
where $\textrm{Z}_t$ is the random gradient
$$
\textrm{Z}_t = \frac{1}{B} \sum_{i=1}^B \nabla_{\boldsymbol{\theta}} L\left({\bf y}_{i} , \alpha\Big( \vec{f}(\textrm{s}_i \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}_t) ; \boldsymbol{\theta}^{(\alpha)}_t \Big) \right)
$$
with $\boldsymbol{\theta} = (\boldsymbol{\theta}^{(\alpha)}, \boldsymbol{\theta}^{(f)})$, with the random permutations $\{\textrm{s}_i\}_{i=1}^B$, $\textrm{s}_i \sim \text{Uniform}(\mathbb{S}_{|{\bf x}^{(i)}|})$; the learning rate is $\eta_t \in (0,1)$ s.t. $\sum_{t=1}^\infty \eta_t = \infty$ and $\sum_{t=1}^\infty \eta_t^2 < \infty$.
Proposition 2.2 (Murphy et al., 2019): $\pi$-SGD is a stochastic optimization procedure with following objective (loss) function: $$\begin{align}\label{eq:RLoss} \tag{9} J(\mathcal{D};\boldsymbol{\theta}^{(\alpha)}, \boldsymbol{\theta}^{(f)}) &= \frac{1}{N}\sum_{i=1}^N E_{\textrm{s}_i}\left[ \! L\Bigg({\bf y}_i , \alpha\Big( \vec{f}(\textrm{s}_i \circ {\bf x}^{(i)};\boldsymbol{\theta}^{(f)}) ; \boldsymbol{\theta}^{(\alpha)} \Big) \Bigg) \right]\\ &= \frac{1}{N}\sum_{i=1}^N \frac{1}{n^{(i)}!} \sum_{\pi \in \mathbb{S}_{|{\bf x}^{(i)}|}} L\Bigg({\bf y}_i , \alpha\Big( \vec{f}(\pi \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}) ; \boldsymbol{\theta}^{(\alpha)} \Big) \Bigg), \end{align}$$
Compare the original loss: $$\overline{\overline{L}}(\mathcal{D};\boldsymbol{\theta}^{(\rho)},\boldsymbol{\theta}^{(f)}) = \frac{1}{N}\sum_{i=1}^N \! L\left({\bf y}_i , \rho\Big( \Gamma({\bf x}^{(i)};\boldsymbol{\theta}^{(f)}) ; \boldsymbol{\theta}^{(\rho)} \Big) \right) ,$$ where $$\Gamma({\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}) = \frac{1}{n^{(i)}!} \sum_{\pi \in \mathbb{S}_{|{\bf x}^{(i)}|}} \!\!\vec{f}(n^{(i)}, \pi \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}).$$
with the new objective: $$J(\mathcal{D};\boldsymbol{\theta}^{(\alpha)}, \boldsymbol{\theta}^{(f)}) = \frac{1}{N}\sum_{i=1}^N \frac{1}{n^{(i)}!} \sum_{\pi \in \mathbb{S}_{|{\bf x}^{(i)}|}} L\Bigg({\bf y}_i , \alpha\Big( \vec{f}(\pi \circ {\bf x}^{(i)}; \boldsymbol{\theta}^{(f)}) ; \boldsymbol{\theta}^{(\alpha)} \Big) \Bigg).$$
Observe that the expectation over permutations is now outside the $L$ and $\alpha$ functions.
In general, the optima of $J$ are different from those of the original objective function $\overline{\overline{L}}$.
Inference of models trained with $\pi$-SGD: The use of $\pi$-SGD to optimize the the original loss optimizes the new objective in Equation (9), and thus has the following implication on how outputs should be calculated at inference time:
(Murphy et al., 2019) Ryan L. Murphy, Balasubramaniam Srinivasan, Vinayak Rao, and Bruno Ribeiro, "Janossy Pooling: Learning Deep Permutation-invariant Functions for Variable-size Inputs", ICLR 2019.
(Sabour et al., 2017) Sara Sabour, Nicholas Frosst, and Geoffrey E. Hinton. "Dynamic routing between capsules." NeurIPS 2017.
(Bahdanau et al., 2015) Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. "Neural machine translation by jointly learning to align and translate." ICLR 2015.
(Zaheer et al., 2017) Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Ruslan Salakhutdinov, and Alexander Smola. "Deep sets". NeurIPS 2017.
(Vinyals et al., 2016) Oriol Vinyals, Samy Bengio, and Manjunath Kudlur. Order Matters: Sequence to Sequence for Sets. ICLR, 2016
(Lee et al., 2019) Lee, Juho, Yoonho Lee, Jungtaek Kim, Adam R. Kosiorek, Seungjin Choi, and Yee Whye Teh. "Set transformer: A framework for attention-based permutation-invariant neural networks." ICML 2019.
(Finzi et al., 2021) Marc Finzi, Max Welling, and Andrew Gordon Wilson. "A Practical Method for Constructing Equivariant Multilayer Perceptrons for Arbitrary Matrix Groups". ICML 2021.
(Puny et al., 2022) Omri Puny, Matan Atzmon, Heli Ben-Hamu, Edward J. Smith, Ishan Misra, Aditya Grover, and Yaron Lipman. "Frame Averaging for Invariant and Equivariant Network Design". ICLR 2022.