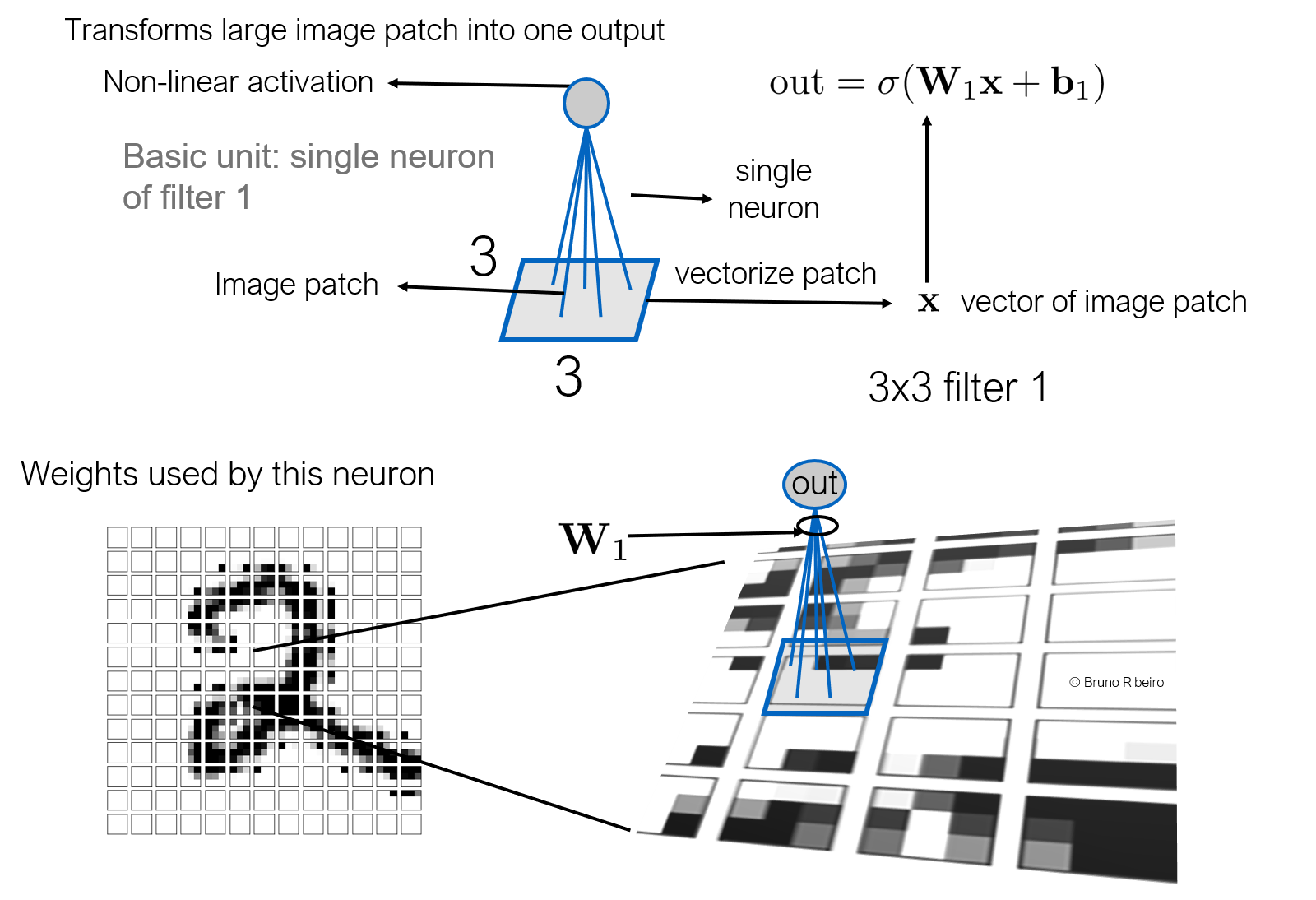
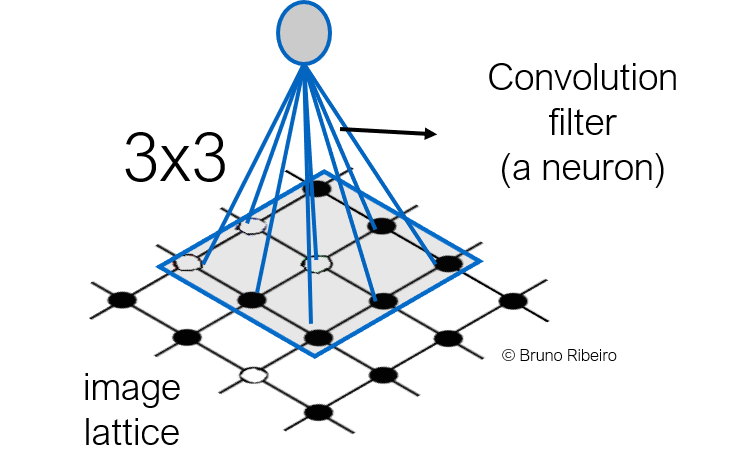
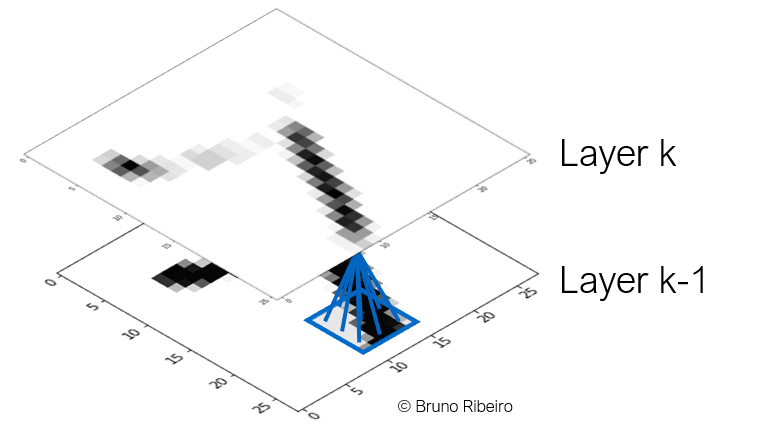
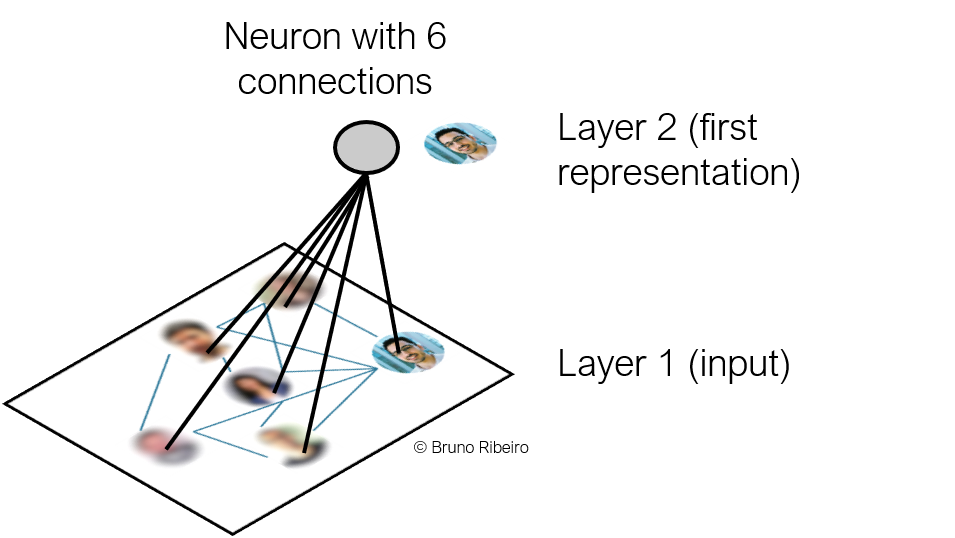
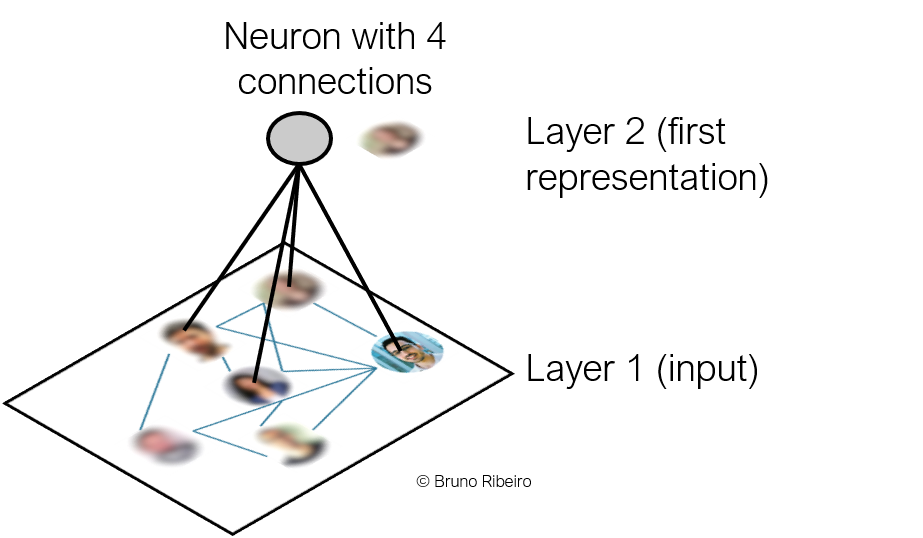
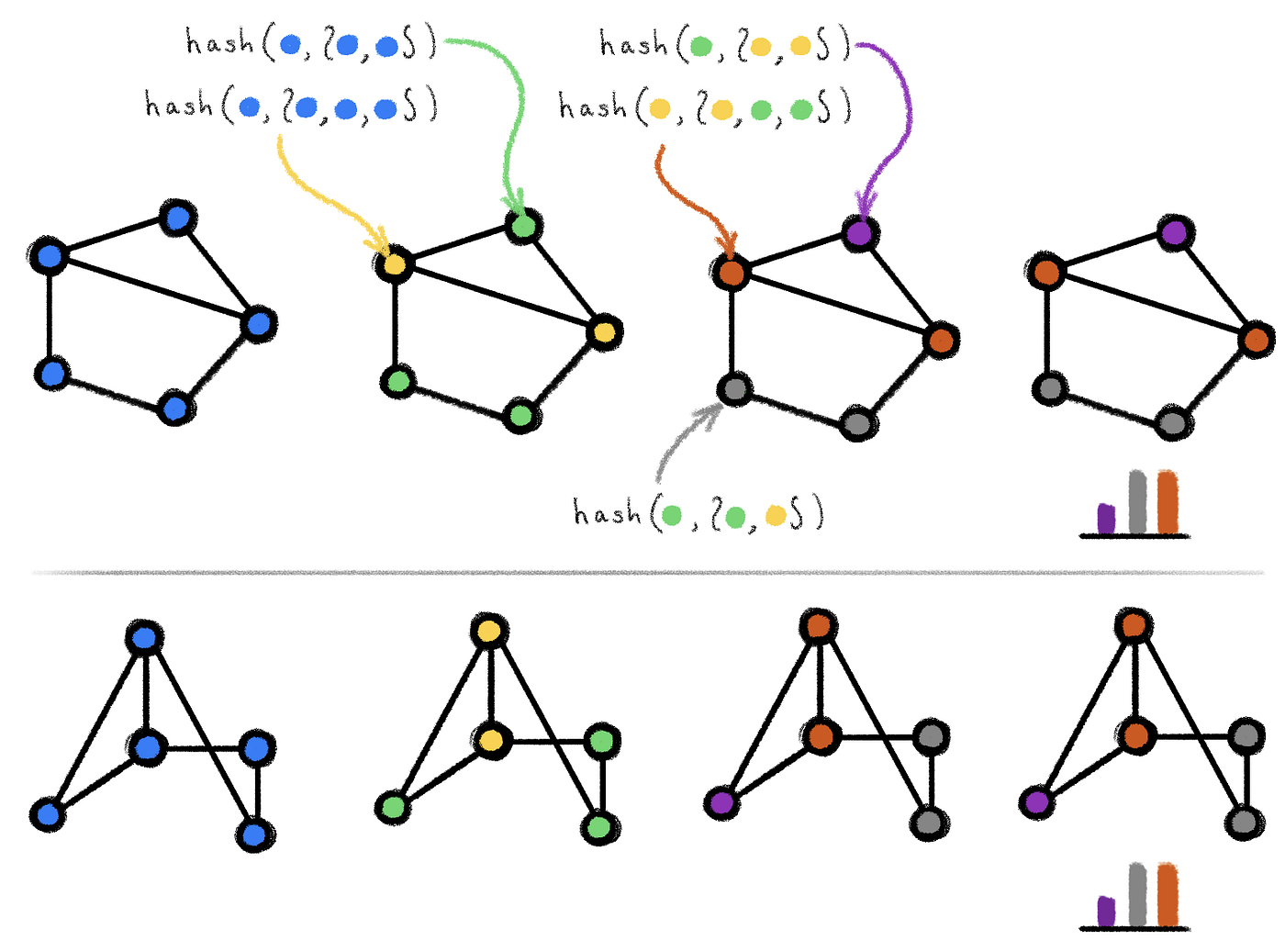
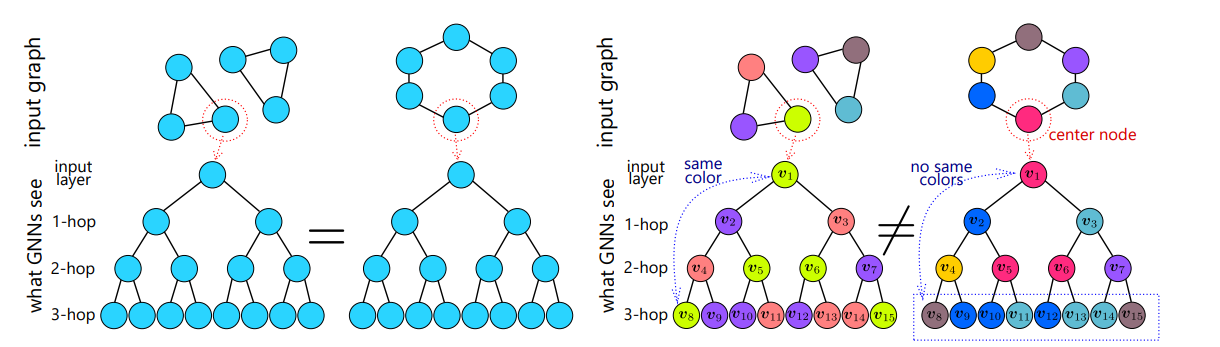
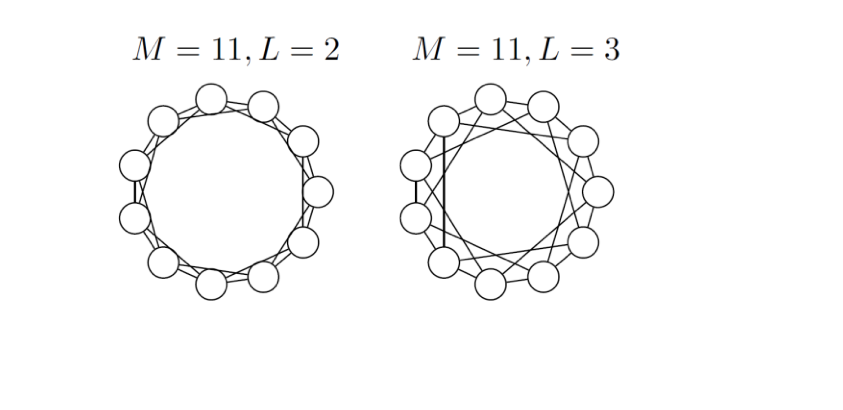References¶
Srinivasan and Ribeiro, 2020. Srinivasan, B., and Ribeiro, B. On the Equivalence between Positional Node Embeddings and Structural Graph Representations. ICLR 2020.
Cotta, Leonardo, Christopher Morris, and Bruno Ribeiro. "Reconstruction for powerful graph representations." Advances in Neural Information Processing Systems 34 (2021): 1713-1726.
Morris et al., 2019. Morris, C., Ritzert, M., Fey, M., Hamilton, W. L., Lenssen, J. E., Rattan, G., and Grohe, M. Weisfeiler and leman go neural: Higher-order graph neural networks. AAAI 2019
Veličković et al., 2018. Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., and Bengio, Y. Graph attention Networks. ICLR 2018
Bahdanau et al., 2015. Bahdanau, D., Cho, K. H., and Bengio, Y. Neural machine translation by jointly learning to align and translate. ICLR 2015
Xu et al., 2019. Xu, K., Hu, W., Leskovec, J., and Jegelka, S. How powerful are graph neural networks? ICLR 2019
Murphy et al., 2019. Murphy, R., Srinivasan, B., Rao., V. and Ribeiro, B. Relational Pooling for Graph Representations. ICML 2019
Maron et al., 2019a. Maron, H., Ben-Hamu, H., Shamir, N., and Lipman, Y. Invariant and Equivariant Graph Networks. ICLR 2019
Maron et al., 2019b. Maron, H., Ben-Hamu, H., Segol, N., and Lipman, Y. On the Universality of Invariant Networks. ICML 2019
Maron et al., 2019c. Maron, H., Ben-Hamu, H., Serviansky, H., and Lipman, Y. Provably powerful graph networks. NeurIPS 2019
Geerts, 2020. Geerts, F. The expressive power of kth-order invariant graph networks. ArXiv Preprint
Abboud et al., 2021. Abboud, R., Ceylan, I. I., Grohe, M., and Lukasiewicz, T. The surprising power of graph neural networks with random node initialization. IJCAI-21
Sato et al., 2021. Sato, R., Yamada, M., and Kashima, H. Random features strengthen graph neural networks. SDM 2021
Chen et al., 2020. Chen, Z., Chen, L., Villar, S., Bruna, J. Can Graph Neural Networks Count Substructures? NeurIPS 2020
Bouritsas et al., 2022. Bouritsas, G., Frasca, F., Zafeiriou, S., and Bronstein, M. M. Improving graph neural network expressivity via subgraph isomorphism counting. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022
Bodnar et al., 2021. Bodnar, C., Frasca, F., Otter, N., Wang, Y. G., Liò, P., Montúfar, G., and Bronstein, M. M. Weisfeiler and lehman go cellular: CW networks. NeurIPS 2021
Cotta et al., 2021. Cotta, L., Morris, C., and Ribeiro, B. Reconstruction for powerful graph representations. NeurIPS 2021
Zhang and Li, 2021. Zhang, M. and Li, P. Nested graph neural networks. NeurIPS 2021
You et al., 2021. You, J., Gomes-Selman, J., Ying, R., and Leskovec, J. Identity-aware graph neural networks. AAAI 2021.
Bevilacqua et al., 2022. Bevilacqua, B., Frasca, F., Lim, D., Srinivasan, D., Cai, C., Balamurugan, G., Bronstein, M. M., Maron, H. Equivariant Subgraph Aggregation Networks. ICLR 2022
Zhao et al., 2022. Zhao, L., Jin, W., Akoglu, L., and Shah, N. From stars to subgraphs: Uplifting any GNN with local structure awareness. ICLR 2022.
Papp et al., 2021. Papp, P. A., Martinkus, K., Faber, L., and Wattenhofer, R. Dropgnn: Random dropouts increase the expressiveness of graph neural networks. NeurIPS 2021
Frasca et al., 2022. Frasca, F., Bevilacqua, B., Bronstein, M. M., Maron, H. Understanding and Extending Subgraph GNNs by Rethinking their Symmetries. NeurIPS 2022
Quian et al., 2022. Qian, C., Rattan, G., Geerts, F., Morris, C., Niepert, M. Ordered Subgraph Aggregation Networks. NeurIPS 2022