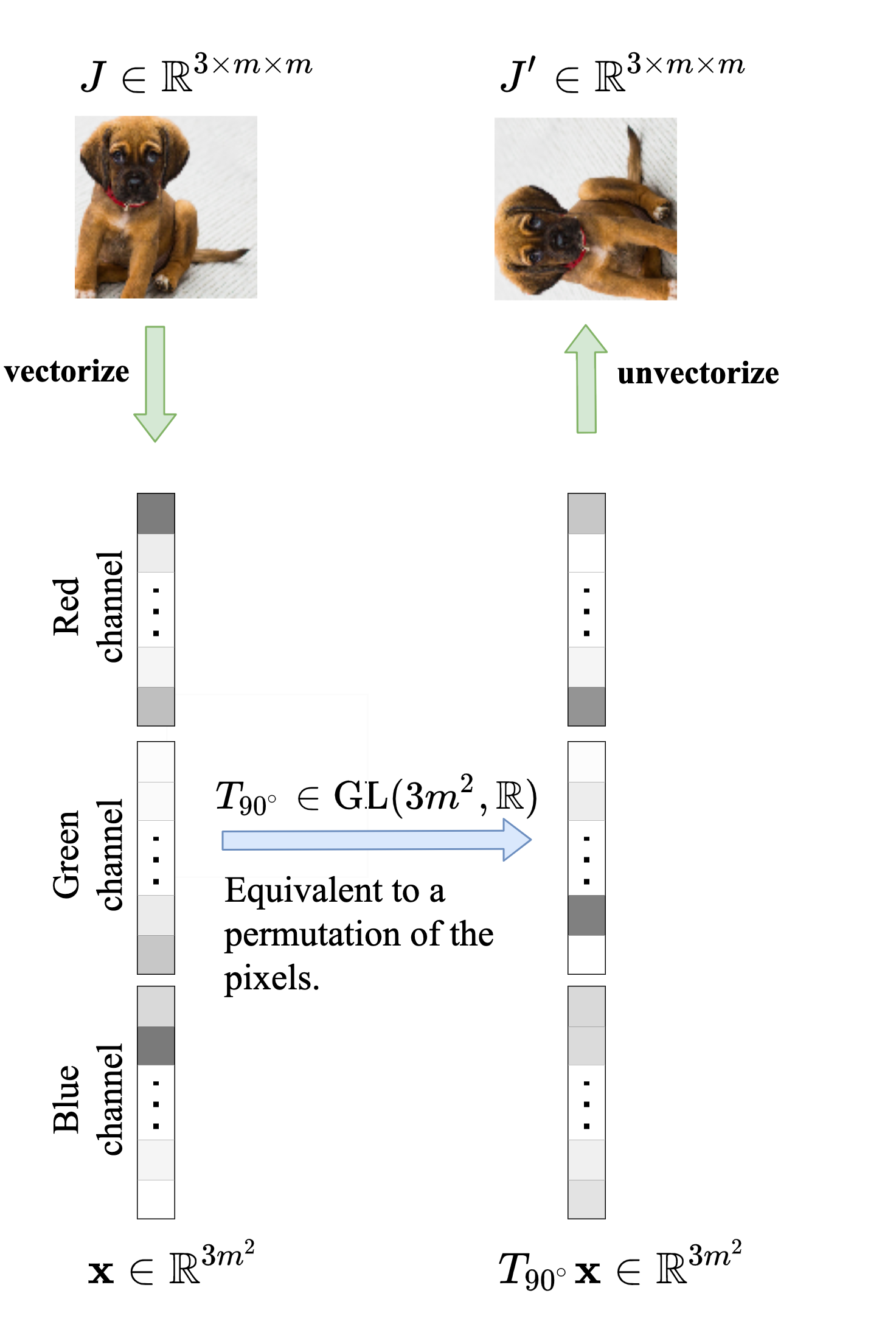
References¶
(Murphy et al., 2019) Ryan L. Murphy, Balasubramaniam Srinivasan, Vinayak Rao, and Bruno Ribeiro, "Janossy Pooling: Learning Deep Permutation-invariant Functions for Variable-size Inputs", ICLR 2019.
(Mouli and Ribeiro, 2021) S. C. Mouli, Bruno Ribeiro, "Neural networks for learning counterfactual G-invariances from single environments". ICLR 2021.
Dmitry Yarotsky, "Universal approximations of invariant maps by neural networks," Constructive Approximations, 2021
(Sabour et al., 2017) Sara Sabour, Nicholas Frosst, and Geoffrey E. Hinton. "Dynamic routing between capsules." NeurIPS 2017.
(Bahdanau et al., 2015) Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. "Neural machine translation by jointly learning to align and translate." ICLR 2015.
(Zaheer et al., 2017) Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Ruslan Salakhutdinov, and Alexander Smola. "Deep sets". NeurIPS 2017.
(Vinyals et al., 2016) Oriol Vinyals, Samy Bengio, and Manjunath Kudlur. Order Matters: Sequence to Sequence for Sets. ICLR, 2016
(Lee et al., 2019) Lee, Juho, Yoonho Lee, Jungtaek Kim, Adam R. Kosiorek, Seungjin Choi, and Yee Whye Teh. "Set transformer: A framework for attention-based permutation-invariant neural networks." ICML 2019.
(Finzi et al., 2021) Marc Finzi, Max Welling, and Andrew Gordon Wilson. "A Practical Method for Constructing Equivariant Multilayer Perceptrons for Arbitrary Matrix Groups". ICML 2021.
(Puny et al., 2022) Omri Puny, Matan Atzmon, Heli Ben-Hamu, Edward J. Smith, Ishan Misra, Aditya Grover, and Yaron Lipman. "Frame Averaging for Invariant and Equivariant Network Design". ICLR 2022.